728x90
https://www.acmicpc.net/problem/11729
알고리즘 설명
문제 설명
이 문제는 유명한 하노이의 탑(Tower of Hanoi) 문제입니다.
세 개의 장대와 여러 개의 원판을 사용하여 특정 규칙을 따라 첫 번째 장대에 있는 원판을 세 번째 장대로 옮기는 문제입니다.
각 원판은 크기가 다르고, 큰 원판은 작은 원판 아래에만 놓일 수 있습니다.
한 번에 하나의 원판만 이동할 수 있으며, 더 큰 원판은 작은 원판 위에 올려 놓을 수 없습니다.
하노이 탑의 이동 횟수는 2 ^ n - 1 로 잘 알려져 있습니다.
이 문제는 그 이동 횟수와 이동 순서를 구하는 문제입니다.
풀이를 3번 했는데,
앞선 두번의 풀이를 하고나면 좋은 방법이 떠올라서 한번씩 더 풀었습니다.
코드 설명 1
from copy import deepcopy
n = int(input())
def hanoi(x):
# 1, 2 인 경우 하드 코딩
if x == 1:
return [[1, 3]]
if x == 2:
return [[1, 2], [1, 3], [2, 3]]
# 재귀의 방식 : 1에서 3으로 옮기는게 아니라
# 1에서 2로 x-1개 옮기고 1에서 3으로 x번째 제일 큰거 옮기고
# 다시 2에서 3으로 옮기는 방식
tmp1 = hanoi(x - 1)
tmp2 = deepcopy(tmp1)
A = [] # 1에서 2로 x-1개를 옮기는 경우
B = [] # 2에서 3으로 x-1개를 옮기는 경우
# A에서 2와 3을 바꿔주고
# B에서는 1이랑 2를 바꿔준다
for i in range(len(tmp1)):
for j in range(2):
if tmp1[i][j] == 2 or tmp1[i][j] == 3:
tmp1[i][j] = 5 - tmp1[i][j]
if tmp2[i][j] == 1 or tmp2[i][j] == 2:
tmp2[i][j] = 3 - tmp2[i][j]
A.append(tmp1[i])
B.append(tmp2[i])
return A + [[1, 3]] + B
res = hanoi(n)
print(len(res))
for tmp in res:
print(*tmp)hanoi(x) 함수는 원판 x개를 1번 막대에서 3번 막대로 옮기는 과정을 반환해줌니다.
원판이 1개, 2개일 때 는 각각 경우의 수가 1개, 3개 이므로 하드코딩을 했습니다.
x개의 이동을 구할 때,
- x - 1개를 2번으로 옮기고
- 가장 큰 1개를 3번으로 옮기고
- x - 1개를 3번으로 옮기고
의 과정을 구현했습니다.
코드 설명 2
ans = {}
# number, 시작, 끝, 중간
def hanoi(x, s1, s2, s3):
key = (x, s1, s2, s3)
# 이미 계산한 값이면 반환
if key in ans:
return ans[key]
# x = 1인 경우 하드 코딩
if x == 1:
return [s1, s2]
# 위의 코드와 마찬가지로 x - 1 번째의 값을 구해서 더해주는 방식
# 앞의 경우는 중간과 끝을 바꿔서 계산하는 경우
# + 젤 큰거 옮기기
# 뒤의 경우는 시작과 중간을 바꿔서 계산하는 경우
# 다음에 또 계산하는 것을 피하기 위해 딕셔너리에 저장
tmp = hanoi(x - 1, s1, s3, s2) + [s1, s2] + hanoi(x - 1, s3, s2, s1)
ans[key] = tmp
return tmp
n = int(input())
res = hanoi(n, 1, 3, 2)
print(2 ** n - 1)
for i in range(2 ** n - 1):
print(res[2 * i], res[2 * i + 1])코드의 알고리즘 구성방식은 같습니다.
다른 점은 메모이제이션을 사용하여 중복되는 계산을 피했다는 점입니다.
코드 설명 3
ans = {}
def hanoi(x, board1, board3, board2):
key = (x, board1, board3, board2)
if key in ans:
return ans[key]
if x == 1:
return f'{board1} {board3}'
tmp = '\n'.join([hanoi(x - 1, board1, board2, board3), f'{board1} {board3}', hanoi(x - 1, board2, board3, board1)])
ans[key] = tmp
return tmp
n = int(input())
res = hanoi(n, '1', '3', '2')
print(2 ** n - 1)
print(res)이 코드는 2번 코드의 리스트 형식의 메모이제이션 및 재귀호출을 문자열을 사용하여 시간을 크게 단축시킨 코드입니다.
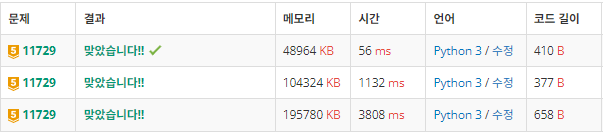
다음은 세 문제의 효율 차이입니다.
반응형
'백준 문제풀이 코드저장소 > Gold' 카테고리의 다른 글
| Baekjoon 7662. 이중 우선순위 큐 / Python (3) | 2024.07.13 |
|---|---|
| Baekjoon 14500. 테트로미노 / Python (2) | 2024.07.13 |
| Baekjoon 1202. 보석 도둑 / Python (1) | 2024.07.10 |
| Baekjoon 30805. 사전 순 최대 공통 부분 순열 / Python (0) | 2024.07.08 |