728x90
일반적인 재귀함수를 통한 피보나치 수열의 구현과는 다른 문제이다. (문제에선 n이 10 ^ 18 이하의 자연수이다.)
우선 수학적으로 피보나치 수열을 구현하는 방식을 알고 있어야 한다.
F(n + 1) = F(n) + F(n - 1)
F(n) = F(n)
을 행렬화 하면
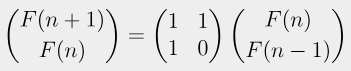
즉,

의 식이 완성된다.
이 식을 구하는 과정은 Linear Algebra의 Diagonalization을 찾아보시길 바랍니다.
이런 공식을 이분 탐색 알고리즘을 위한 식으로 만들 수 있다.

본 풀이는 이 방법을 사용해서 기존 피보나치 재귀함수의 시간복잡도 (O(2 ^ ㅜ))을 O(n)으로 줄이고, 이분 탐색을 통해 이를 다시 O(log n) 으로 줄였다.
N = int(input())
matrix = [[1, 1], [1, 0]]
def mul_matrix(mat1, mat2):
res = [[0]*2 for _ in range(2)]
for i in range(2):
for j in range(2):
for z in range(2):
res[i][j] = (res[i][j] + mat1[i][z] * mat2[z][j]) % 1000000007
return res
def power(a, b):
if b == 1:
return a
else:
tmp = power(a, b // 2)
if b % 2 == 0:
return mul_matrix(tmp, tmp)
else:
return mul_matrix(mul_matrix(tmp, tmp), a)
if N == 0:
print(0)
elif N == 1:
print(1)
else:
result = power(matrix, N-1)
print(result[0][0])반응형
'백준 문제풀이 코드저장소 > Gold' 카테고리의 다른 글
| Baekjoon 1005. ACM Craft / Python (2) | 2024.07.01 |
|---|---|
| Baekjoon 1167. 트리의 지름 / Python (0) | 2024.07.01 |
| Baekjoon 12100. 2048 (Easy) / Python (0) | 2024.07.01 |
| Baekjoon 12015. 가장 긴 증가하는 부분 수열 2 / Python (2) | 2024.06.30 |